SMO

3169 days ago by takepwave

SMO system:sage Hiroshi TAKEMOTO (take@pwv.co.jp)

第7章-SVM（サポートベクトルマシン）をSageで試す

今回は、SVMに関する他のサイトの情報を元にSageでSVMを試してみます。 参考（ほとんどコピー）にしたのは以下のサイトです。

上記で説明されたSVMを計算する2通りの方法が7章を理解する上で助けになりました。

テストデータ

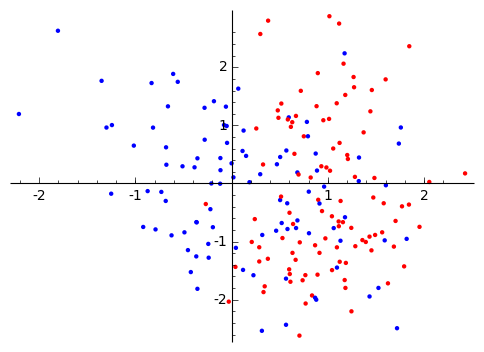
SVMのテストには、PRMLの図7.4、

で使用された（赤と青の点が入り混ざっている）人工データを使います。

カーネルには、$exp(-\gamma||x - x'||^2)$のガウスカーネルを使い、$\gamma=0.45$とします。

# SMOで識別を行う from numpy import loadtxt data = loadtxt(DATA+"classification.txt") # 1,2カラムはx, y、3カラムには、0:red cosses×, 1:blue circle ○がセットされている # これをx, yと識別子(-1, 1)に変換する X = [[x[0], x[1]] for x in data[:,0:2]] T = data[:,2]*2-1 
       
var('x y') data_plt = Graphics() for i in range(len(T)): if T[i] == -1: data_plt += point(X[i], rgbcolor='red') else: data_plt += point(X[i], rgbcolor='blue') data_plt.show(figsize=5) 
       

SMO

「きちめも」で実装されている、「サポートベクターマシン入門」の付録に掲載されているSMO(Sequenctial Minimal Optimization) は、J. Platt(1988)で発表されたもので、2つのデータ点に対する最適化問題を解析的に求め、ヒューリスティクスな選択で反復的な処理を 高速に収束させる手法です。

以下では、「きちめも」の実装に若干の修正を加えています。

  • ガウスカーネルを図7.4の説明に合わせた
  • 「サポートベクターマシン入門」の注釈7.14からcalc_bを_examinExの最後にも追加
  • KKTのチェックは、「サポートベクターマシン入門」の付録Aに合わせた。 しかし後のCVXOPTの例を見るとサポートベクトルの抽出には、αの許容する誤差が必要みたいです。
# se-kichiさんの「きちめも」から引用 # http://d.hatena.ne.jp/se-kichi/20100306/1267858745#20100306f1 # 修正点： _searchのelse jをelse kに変更 # 「サポートベクターマシン入門」の注釈7.14からcalc_bを_examinExの最後にも追加 # KKTのチェックにself._epsが含まれているが、「サポートベクターマシン入門」の付録Aに合わせた import random from scipy import zeros, array from scipy.linalg import norm as _norm class SMO: """ Support Vector Machine using SMO Algorithm. """ def __init__(self, kernel=lambda x,y:dot(x,y), c=10000, tol=1e-2, eps=1e-2, loop=float('inf')): """ Arguments: - `kernel`: カーネル関数 - `c`: パラメータ - `tol`: KKT条件の許容する誤差 - `eps`: αの許容する誤差 - `loop`: ループの上限 """ self._kernel = kernel self._c = c self._tol = tol self._eps = eps self._loop = loop def _takeStep(self, i1, i2): if i1 == i2: return False alph1 = self._alpha[i1] alph2 = self._alpha[i2] y1 = self._target[i1] y2 = self._target[i2] e1 = self._e[i1] e2 = self._e[i2] s = y1 * y2 if y1 != y2: L = max(0, alph2 - alph1) H = min(self._c, self._c-alph1+alph2) else: L = max(0, alph2 + alph1 - self._c) H = min(self._c, alph1+alph2) if L == H: return False k11 = self._kernel(self._point[i1], self._point[i1]) k12 = self._kernel(self._point[i1], self._point[i2]) k22 = self._kernel(self._point[i2], self._point[i2]) eta = 2 * k12 - k11 - k22 if eta > 0: return False a2 = alph2 - y2 * (e1 - e2) / eta a2 = min(H, max(a2, L)) if abs(a2 - alph2) < self._eps * (a2 + alph2 + self._eps): return False a1 = alph1 + s * (alph2 - a2) # update da1 = a1 - alph1 da2 = a2 - alph2 self._e += array([(da1 * self._target[i1] * self._kernel(self._point[i1], p) + da2 * self._target[i2] * self._kernel(self._point[i2], p)) for p in self._point]) self._alpha[i1] = a1 self._alpha[i2] = a2 return True def _search(self, i, lst): if self._e[i] >= 0: return reduce(lambda j,k: j if self._e[j] < self._e[k] else k, lst) else: return reduce(lambda j,k: j if self._e[j] > self._e[k] else k, lst) def _examinEx(self, i2): y2 = self._target[i2] alph2 = self._alpha[i2] e2 = self._e[i2] r2 = e2*y2 if ((r2 < -self._tol and alph2 < self._c) or (r2 > self._tol and alph2 > 0)): alst1 = [i for i in range(len(self._alpha)) if 0 < self._alpha[i] < self._c] if alst1: i1 = self._search(i2, alst1) if self._takeStep(i1, i2): return True random.shuffle(alst1) for i1 in alst1: if self._takeStep(i1, i2): return True alst2 = [i for i in range(len(self._alpha)) if (self._alpha[i] <= 0 or self._alpha[i] >= self._c)] random.shuffle(alst2) for i1 in alst2: if self._takeStep(i1, i2): return True # 注釈7.14にtakeStepでbの更新は必要ないが、停止基準を評価する場合には必要とのコメントから挿入 self._calc_b() return False def _calc_b(self): self._s = [i for i in range(len(self._target)) if 0 < self._alpha[i]] self._m = [i for i in range(len(self._target)) if 0 < self._alpha[i] < self._c] self._b = 0.0 for i in self._m: self._b += self._target[i] for j in self._s: self._b -= (self._alpha[j]*self._target[j]* self._kernel(self._point[i], self._point[j])) self._b /= len(self._m) def calc(self, x): ret = self._b for i in self._s: ret += (self._alpha[i]*self._target[i]* self._kernel(x, self._point[i])) return ret def learn(self, point, target): self._target = target self._point = point self._alpha = zeros(len(target), dtype=float) self._b = 0 self._e = -1*array(target, dtype=float) changed = False examine_all = True count = 0 while changed or examine_all: count += 1 if count > self._loop: break changed = False if examine_all: for i in range(len(self._target)): changed |= self._examinEx(i) else: for i in (j for j in range(len(self._target)) if 0 < self._alpha[j] < self._c): changed |= self._examinEx(i) if examine_all: examine_all = False elif not changed: examine_all = True self._calc_b() def _get_s(self): return self._s def _get_m(self): return self._m def _get_alpha(self): return self._alpha 
       
# numpyのnormは、ベクトルの絶対値を返すから自乗する import numpy as np N = len(T) C = 30 def kernel(x, y): return np.exp(-0.45*_norm(x-y)**2) s = SMO(c=C, kernel=kernel, loop=20) p = data[:,0:2] t = data[:,2]*2-1.0 s.learn(p, t) 
       

SMOの計算結果

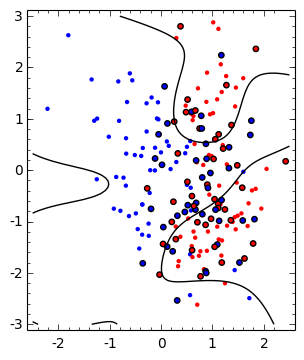
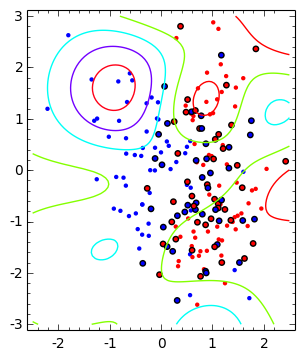
SMOの計算結果は、図7.4と同様のパターンを得ました。

  • 最初の図は、境界線（黒線）とサポートベクタ（縁取りした大きな点）
  • コンター図で分布パターンを示したもの
# コンター図を作成 cnt_plt = contour_plot(lambda x, y : s.calc([x, y]), [x, -2.5, 2.5], [y, -3, 3], contours=(0.0,), fill=False) # サポートベクターのポイントを強調して表示 sv_plt = Graphics() for i in s._get_s(): if T[i] == -1: sv_plt += point(X[i], rgbcolor='red', pointsize=15, faceted=True) else: sv_plt += point(X[i], rgbcolor='blue', pointsize=15, faceted=True) (cnt_plt + data_plt + sv_plt).show(figsize=5) 
       
# コンター図を作成 cnt_plt = contour_plot(lambda x, y : s.calc([x, y]), [x, -2.5, 2.5], [y, -3, 3], fill=False, cmap='hsv') (cnt_plt + data_plt + sv_plt).show(figsize=5) 
       

CVXOPTを使ったSVM

「人工知能に関する断想録」では、適化ライブラリCVXOPTを使ってSVMを計算しています。

「人工知能に関する断想録」のポイントは、CVXOPTの入力形式に $$ \begin{array}{ll} \mbox{minimize} & (1/2)x^TPx + q^Tx \\ \mbox{subject to} & G x \leq h \\ & A x = b \end{array} $$ 制約条件$0 \le a_n \le C$をどうやって組み入れるかですが、 $$ G x \leq h $$ を $$ \begin{pmatrix} -1 & 0 \\ 0 & -1 \\ 1 & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} a_1\\ a_2 \end{pmatrix} \le \begin{pmatrix} 0 \\ 0 \\ C \\ C \end{pmatrix} $$ とすることで解決されたそうです。

「人工知能に関する断想録」からの変更点は

  • 「人工知能に関する断想録」のコメントからサポートベクタの抽出条件を $ \epsilon \le a_n$に変更しました。

# 同様の計算をCVXOPTを使って計算する例 # 「人工知能に関する断想録」から引用 # http://d.hatena.ne.jp/aidiary/20100503/1272889097 X = data[:,0:2] t = data[:,2]*2-1.0 
       
from cvxopt import solvers from cvxopt.base import matrix as _matrix 
       
def f(x, a, t, X, b): sum = 0.0 for n in range(N): sum += a[n] * t[n] * kernel(x, X[n]) return sum + b 
       
# ラグランジュ乗数を二次計画法（Quadratic Programming）で求める K = np.zeros((N, N)) for i in range(N): for j in range(N): K[i, j] = t[i] * t[j] * kernel(X[i], X[j]) Q = _matrix(K) p = _matrix(-np.ones(N)) temp1 = np.diag([-1.0]*N) temp2 = np.identity(N) G = _matrix(np.vstack((temp1, temp2))) temp1 = np.zeros(N) temp2 = np.ones(N) * C h = _matrix(np.hstack((temp1, temp2))) A = _matrix(t, (1,N)) b = _matrix(np.array([[1.0]])) sol = solvers.qp(Q, p, G, h, A, b) a = array(sol['x']).reshape(N) #print a # サポートベクトルのインデックスを抽出 S = [] M = [] # aidiaryさんのコメントを反映して、αの誤差としてepsに1e-3を使用するように変更 eps = 1e-3 for n in range(len(a)): if eps < a[n]: S.append(n) if eps < a[n] < C: M.append(n) # bを計算 sum = 0.0 for n in M: sum = t[n] for m in S: sum -= a[m] * t[m] * kernel(p[n], p[m]) b = sum / len(M) #print S, b 
        
     pcost       dcost       gap    pres   dres
 0:  5.5960e+01 -7.6903e+04  9e+04  1e-01  4e-14
 1: -1.2616e+03 -1.1595e+04  1e+04  1e-02  3e-14
 2: -2.0141e+03 -4.1694e+03  2e+03  2e-03  3e-14
 3: -2.3490e+03 -3.5920e+03  1e+03  8e-04  3e-14
 4: -2.5794e+03 -3.0567e+03  5e+02  3e-04  3e-14
 5: -2.6539e+03 -2.9363e+03  3e+02  1e-04  3e-14
 6: -2.7063e+03 -2.8304e+03  1e+02  5e-05  3e-14
 7: -2.7337e+03 -2.7873e+03  5e+01  1e-05  4e-14
 8: -2.7496e+03 -2.7604e+03  1e+01  2e-06  4e-14
 9: -2.7532e+03 -2.7548e+03  2e+00  2e-07  4e-14
10: -2.7538e+03 -2.7538e+03  8e-02  8e-09  4e-14
11: -2.7538e+03 -2.7538e+03  1e-03  9e-11  4e-14
Optimal solution found.
     pcost       dcost       gap    pres   dres
 0:  5.5960e+01 -7.6903e+04  9e+04  1e-01  4e-14
 1: -1.2616e+03 -1.1595e+04  1e+04  1e-02  3e-14
 2: -2.0141e+03 -4.1694e+03  2e+03  2e-03  3e-14
 3: -2.3490e+03 -3.5920e+03  1e+03  8e-04  3e-14
 4: -2.5794e+03 -3.0567e+03  5e+02  3e-04  3e-14
 5: -2.6539e+03 -2.9363e+03  3e+02  1e-04  3e-14
 6: -2.7063e+03 -2.8304e+03  1e+02  5e-05  3e-14
 7: -2.7337e+03 -2.7873e+03  5e+01  1e-05  4e-14
 8: -2.7496e+03 -2.7604e+03  1e+01  2e-06  4e-14
 9: -2.7532e+03 -2.7548e+03  2e+00  2e-07  4e-14
10: -2.7538e+03 -2.7538e+03  8e-02  8e-09  4e-14
11: -2.7538e+03 -2.7538e+03  1e-03  9e-11  4e-14
Optimal solution found.

CVXOPTの計算結果

CVXOPTの計算は、SMOよりも高速で解も安定しています。

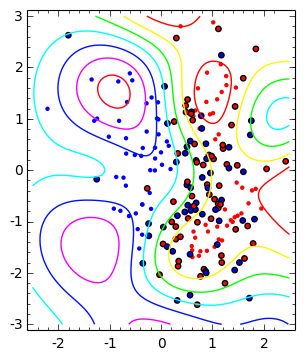
CVXOPTの計算結果も、図7.4と同様のパターンを得ました。

  • 最初の図は、境界線（黒線）とサポートベクタ（縁取りした大きな点）
  • コンター図で分布パターンを示したもの
qp_plt = contour_plot(lambda x, y : f([x, y], a, t, X, b), [x, -2.5, 2.5], [y, -3, 3], fill=False, cmap='hsv') 
       
# サポートベクターのポイントを強調して表示 sv2_plt = Graphics() for i in S: if T[i] == -1: sv2_plt += point(X[i], rgbcolor='red', pointsize=15, faceted=True) else: sv2_plt += point(X[i], rgbcolor='blue', pointsize=15, faceted=True) 
       
(qp_plt + data_plt + sv2_plt).show(figsize=5)