準備
Sageで回帰分析の説明をするために必要な前準備を以下で行います。
# Rのユーティリティ関数を読み込む
attach(DATA+'RUtil.py')
# プロット関数定義
def showPlot(f):
f.show(aspect_ratio=1, figsize=(5), xmin=-1, xmax=1, ymin=-1, ymax=1)
|
|
回帰分析の注意点
大きな母集団から少ないサンプルを抽出して回帰分析を行う場合、以下のような問題点があります。
- モデルがサンプルに合いすぎる（オーバーフィッティング）問題
- 属性を絞り込む場合、最適なモデルの選択問題
オーバーフィッティングの例
サンプルデータ以下の様な関係を持つとします。 $$ f(x, a) = a_0 + a_1 x $$
ここで、$a_0 = -0.3, a_1 = 0.5$とし、一様部分$U(x|-1,1)$から選んだ$x_n$に、目的値$t_n$に 分散0.3の正規分布の誤差を追加します。 $$ t_n = f(x_n, a) + \mathcal{N}(0, 0.3) $$
# データセット f(x, a) = a0 + a1*x <= a0 = -0.3, a1=0.5
a0 = -0.3;
a1 = 0.5;
# f(x)のプロット
x = var('x')
a_plt = plot(a0 + a1*x, [x, -1, 1], rgbcolor ='red')
|
|
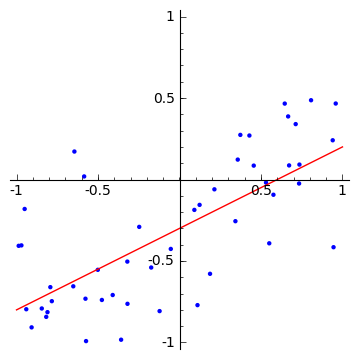
母集団として50個のサンプルデータを作成して、その結果を$f(x,a)$の直線と一緒にプロットしてみます。
データ数が50個の場合には、データにフィットする直線を人の直感で引いた場合とオリジナルの関数$f(x,a)$（赤の直線）はほぼ一致します。
# 観測値は、tn = f(x,a) + N(0, 0.3)
#xv = [];
#tv = [];
#for xn in range(50):
# xn = 2*random() - 1;
# xv += [xn];
# tv += [a0 + a1*xn + gauss(0, 0.3)]
#save(xv, DATA+'xv')
#save(tv, DATA+'tv')
xv = load(DATA+'xv')
tv = load(DATA+'tv')
data = zip(xv, tv);
data_plt = list_plot(zip(xv, tv));
showPlot(a_plt + data_plt)
|
|
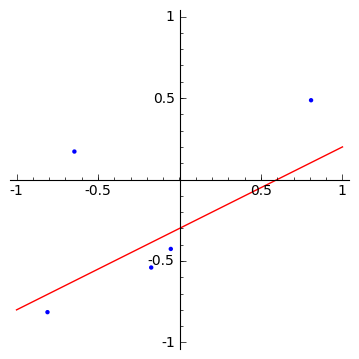
50個の母集団から5個のサンプルを抽出すた場合、オリジナルの関数$f(x,a)$からはずれた分布になります。
# 5点を抽出して
data = zip(xv[10:15],tv[10:15])
showPlot(a_plt + list_plot(data))
|
|
<H3>少ないサンプルから求めた最適な直線</H3>
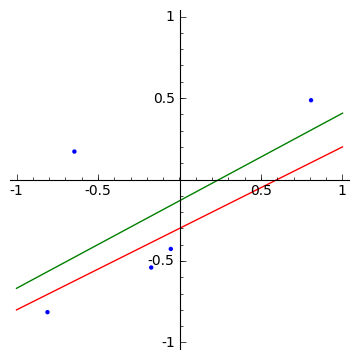
試しに、少ないサンプルから求めた最適な直線を求めています（緑の直線）。
少ないサンプルから求めた最適な直線はオリジナルの関数からずれたり、異なった形になるため、サンプルに合いすぎるのを防ぐ必要があります。
このように回帰分析の結果がサンプルに合いすぎることをオーバーフィッティングと呼びます。
# 5点のサンプルから最適直線を求める
(a0,a1) = var('a0 a1')
model(x) = a0 + a1*x
fit = find_fit(data, model, solution_dict=True); view(fit)
\newcommand{\Bold}[1]{\mathbf{#1}}\left\{a_{0} : -0.130440448397, a_{1} : 0.537229455444\right\}
\newcommand{\Bold}[1]{\mathbf{#1}}\left\{a_{0} : -0.130440448397, a_{1} : 0.537229455444\right\}
|
# 結果の表示
f_fit(x) = model.subs(fit)
fit_plt = plot(f_fit, [x,-1,1], rgbcolor='green')
showPlot(fit_plt + a_plt + list_plot(data))
|
|
Rの線形回帰パッケージ
Rの線形回帰パッケージとして、lmパッケージを使用します。
lmでは、回帰分析の対象の変数を目的変数と呼び、回帰に使用する変数を説明変数と呼んでいます。
lmの最初の引数には、目的変数と説明変数の関係を以下の様な形式で指定します。
目的変数 ~ 説明変数1 + 説明変数2 + ... + 説明変数k
lmを使った直線回帰の例
直線回帰のテストデータとして、女性の身長と体重のサンプルデータwomenを使用して直線回帰を実施してみます。
回帰の結果は、fit変数に保存され、summary関数で回帰の結果を確認できます。
回帰の結果求まった係数（Estimate列）がどの程度重要なのかは、行の最後の重要度（***）の部分で判断できます。★が多いほど重要であることを示しています。
このようにlmパッケージを使った線形回帰分析では、係数の算出だけでなく、その重要度までも含めた情報を出力します。
# Rの線形回帰パッケージを使った分析
r('fit <- lm(weight ~ height, data=women)')
r('summary(fit)')
Call:
lm(formula = weight ~ height, data = women)
Residuals:
Min 1Q Median 3Q Max
-1.7333 -1.1333 -0.3833 0.7417 3.1167
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -87.51667 5.93694 -14.74 1.71e-09 ***
height 3.45000 0.09114 37.85 1.09e-14 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.525 on 13 degrees of freedom
Multiple R-squared: 0.991, Adjusted R-squared: 0.9903
F-statistic: 1433 on 1 and 13 DF, p-value: 1.091e-14
Call:
lm(formula = weight ~ height, data = women)
Residuals:
Min 1Q Median 3Q Max
-1.7333 -1.1333 -0.3833 0.7417 3.1167
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -87.51667 5.93694 -14.74 1.71e-09 ***
height 3.45000 0.09114 37.85 1.09e-14 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.525 on 13 degrees of freedom
Multiple R-squared: 0.991, Adjusted R-squared: 0.9903
F-statistic: 1433 on 1 and 13 DF, p-value: 1.091e-14
|
graph = preGraph("fig8_1.pdf")
r('plot(women$height, women$weight,xlab="Height (in inches)",ylab="Weight (in pounds)")')
r('abline(fit)')
postGraph(graph, fac=0.5)
|
|
# 多重回帰分析の例
# r('install.packages("car")')
r('library(car)')
[1] "car" "nnet" "MASS" "stats" "graphics" "grDevices" "utils" "datasets" [9] "methods" "base" [1] "car" "nnet" "MASS" "stats" "graphics" "grDevices" "utils" "datasets" [9] "methods" "base" |
分析用のデータ
多重回帰分析のテストデータとして、Rに付属するアメリカ合衆国のstate.x77の中から、犯罪率（Murder）、人口（Population）、識字率（Illiteracy）、平均収入（Income）、真冬日の日数（Frost）を取り出し、犯罪率との関係を回帰分析で求めます。
# データを用意する
r('states <- as.data.frame(state.x77[,c("Murder", "Population","Illiteracy", "Income", "Frost")])')
Murder Population Illiteracy Income Frost Alabama 15.1 3615 2.1 3624 20 Alaska 11.3 365 1.5 6315 152 Arizona 7.8 2212 1.8 4530 15 Arkansas 10.1 2110 1.9 3378 65 California 10.3 21198 1.1 5114 20 Colorado 6.8 2541 0.7 4884 166 Connecticut 3.1 3100 1.1 5348 139 Delaware 6.2 579 0.9 4809 103 Florida 10.7 8277 1.3 4815 11 Georgia 13.9 4931 2.0 4091 60 Hawaii 6.2 868 1.9 4963 0 Idaho 5.3 813 0.6 4119 126 Illinois 10.3 11197 0.9 5107 127 Indiana 7.1 5313 0.7 4458 122 Iowa 2.3 2861 0.5 4628 140 Kansas 4.5 2280 0.6 4669 114 Kentucky 10.6 3387 1.6 3712 95 Louisiana 13.2 3806 2.8 3545 12 Maine 2.7 1058 0.7 3694 161 Maryland 8.5 4122 0.9 5299 101 Massachusetts 3.3 5814 1.1 4755 103 Michigan 11.1 9111 0.9 4751 125 Minnesota 2.3 3921 0.6 4675 160 Mississippi 12.5 2341 2.4 3098 50 Missouri 9.3 4767 0.8 4254 108 Montana 5.0 746 0.6 4347 155 Nebraska 2.9 1544 0.6 4508 139 Nevada 11.5 590 0.5 5149 188 New Hampshire 3.3 812 0.7 4281 174 New Jersey 5.2 7333 1.1 5237 115 New Mexico 9.7 1144 2.2 3601 120 New York 10.9 18076 1.4 4903 82 North Carolina 11.1 5441 1.8 3875 80 North Dakota 1.4 637 0.8 5087 186 Ohio 7.4 10735 0.8 4561 124 Oklahoma 6.4 2715 1.1 3983 82 Oregon 4.2 2284 0.6 4660 44 Pennsylvania 6.1 11860 1.0 4449 126 Rhode Island 2.4 931 1.3 4558 127 South Carolina 11.6 2816 2.3 3635 65 South Dakota 1.7 681 0.5 4167 172 Tennessee 11.0 4173 1.7 3821 70 Texas 12.2 12237 2.2 4188 35 Utah 4.5 1203 0.6 4022 137 Vermont 5.5 472 0.6 3907 168 Virginia 9.5 4981 1.4 4701 85 Washington 4.3 3559 0.6 4864 32 West Virginia 6.7 1799 1.4 3617 100 Wisconsin 3.0 4589 0.7 4468 149 Wyoming 6.9 376 0.6 4566 173 Murder Population Illiteracy Income Frost Alabama 15.1 3615 2.1 3624 20 Alaska 11.3 365 1.5 6315 152 Arizona 7.8 2212 1.8 4530 15 Arkansas 10.1 2110 1.9 3378 65 California 10.3 21198 1.1 5114 20 Colorado 6.8 2541 0.7 4884 166 Connecticut 3.1 3100 1.1 5348 139 Delaware 6.2 579 0.9 4809 103 Florida 10.7 8277 1.3 4815 11 Georgia 13.9 4931 2.0 4091 60 Hawaii 6.2 868 1.9 4963 0 Idaho 5.3 813 0.6 4119 126 Illinois 10.3 11197 0.9 5107 127 Indiana 7.1 5313 0.7 4458 122 Iowa 2.3 2861 0.5 4628 140 Kansas 4.5 2280 0.6 4669 114 Kentucky 10.6 3387 1.6 3712 95 Louisiana 13.2 3806 2.8 3545 12 Maine 2.7 1058 0.7 3694 161 Maryland 8.5 4122 0.9 5299 101 Massachusetts 3.3 5814 1.1 4755 103 Michigan 11.1 9111 0.9 4751 125 Minnesota 2.3 3921 0.6 4675 160 Mississippi 12.5 2341 2.4 3098 50 Missouri 9.3 4767 0.8 4254 108 Montana 5.0 746 0.6 4347 155 Nebraska 2.9 1544 0.6 4508 139 Nevada 11.5 590 0.5 5149 188 New Hampshire 3.3 812 0.7 4281 174 New Jersey 5.2 7333 1.1 5237 115 New Mexico 9.7 1144 2.2 3601 120 New York 10.9 18076 1.4 4903 82 North Carolina 11.1 5441 1.8 3875 80 North Dakota 1.4 637 0.8 5087 186 Ohio 7.4 10735 0.8 4561 124 Oklahoma 6.4 2715 1.1 3983 82 Oregon 4.2 2284 0.6 4660 44 Pennsylvania 6.1 11860 1.0 4449 126 Rhode Island 2.4 931 1.3 4558 127 South Carolina 11.6 2816 2.3 3635 65 South Dakota 1.7 681 0.5 4167 172 Tennessee 11.0 4173 1.7 3821 70 Texas 12.2 12237 2.2 4188 35 Utah 4.5 1203 0.6 4022 137 Vermont 5.5 472 0.6 3907 168 Virginia 9.5 4981 1.4 4701 85 Washington 4.3 3559 0.6 4864 32 West Virginia 6.7 1799 1.4 3617 100 Wisconsin 3.0 4589 0.7 4468 149 Wyoming 6.9 376 0.6 4566 173 |
分布図で各変数の関連を調べる
carライブラリのscatterplotMatrix関数を使って各変数の関連を調べます。 MurderとIlliteracyに正の相関が見られ、後は判断が難しいように思われます。
# 分布図で関係を見る
graph = preGraph("fig8_4.pdf")
r('scatterplotMatrix(states, spread=FALSE, lty.smooth=2)')
postGraph(graph, fac=0.7)
|
|
多重回帰の結果
lm関数を使って上記のデータの多重回帰分析を行います。
処理は、ほとんど線形回帰と同じです。解析結果のsummaryも分布図から見て取られる傾向と合致し、犯罪率（Murder）には、識字率（Illiteracy）と人口（Population）が関連があることが分かります。
# lmを使った多重回帰
r('fit <- lm(Murder ~ Population + Illiteracy + Income + Frost,data=states)')
r('summary(fit)')
Call:
lm(formula = Murder ~ Population + Illiteracy + Income + Frost,
data = states)
Residuals:
Min 1Q Median 3Q Max
-4.7960 -1.6495 -0.0811 1.4815 7.6210
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.235e+00 3.866e+00 0.319 0.7510
Population 2.237e-04 9.052e-05 2.471 0.0173 *
Illiteracy 4.143e+00 8.744e-01 4.738 2.19e-05 ***
Income 6.442e-05 6.837e-04 0.094 0.9253
Frost 5.813e-04 1.005e-02 0.058 0.9541
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.535 on 45 degrees of freedom
Multiple R-squared: 0.567, Adjusted R-squared: 0.5285
F-statistic: 14.73 on 4 and 45 DF, p-value: 9.133e-08
Call:
lm(formula = Murder ~ Population + Illiteracy + Income + Frost,
data = states)
Residuals:
Min 1Q Median 3Q Max
-4.7960 -1.6495 -0.0811 1.4815 7.6210
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.235e+00 3.866e+00 0.319 0.7510
Population 2.237e-04 9.052e-05 2.471 0.0173 *
Illiteracy 4.143e+00 8.744e-01 4.738 2.19e-05 ***
Income 6.442e-05 6.837e-04 0.094 0.9253
Frost 5.813e-04 1.005e-02 0.058 0.9541
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.535 on 45 degrees of freedom
Multiple R-squared: 0.567, Adjusted R-squared: 0.5285
F-statistic: 14.73 on 4 and 45 DF, p-value: 9.133e-08
|
解析結果のグラフ
解析結果fitをplotすると、予測値と実際の値との残差の関係（左上）、残差のQ-Qプロット（右上）、残差の平方根プロット（左下）、残差と影響力プロット（右下）が表示される。
- 線型モデルがデータを表現できていれば、残差（Residuals）と予測値（Fitted values）はランダムに分布する
- 線型モデルの仮定である残差が正規分布かどうかは、Q-Qプロットが45度の直線に乗っているかどうかで判断する
- 分散を定数だと仮定すると、残差の平方根プロットは、水平線にランダムにプロットされる
- データの中で特に逸脱している（影響を及ぼしている）データをクック距離（Cook's distanceの破線）から推定する。クック距離が0.5以上だと影響力が大きい（例ではAlaska, Nevadaのデータが大きい）
# 回帰結果のプロット例
graph = preGraph("fig8_7.pdf")
r('par(mfrow=c(2,2))')
r('plot(fit)')
postGraph(graph, fac=0.7)
|
|
分析結果の評価
回帰分析の結果から各説明変数が1%変化した場合、目的変数の変化する範囲を95%の確率で求めた結果がconfint関数の結果です。
例えば識字率（Illiteracy）を1%変化させると犯罪率（Murder）は、2.38から5.90の範囲で変化すると予測されます。
# 分析結果の評価
r('confint(fit)')
2.5 % 97.5 % (Intercept) -6.552191e+00 9.0213182149 Population 4.136397e-05 0.0004059867 Illiteracy 2.381799e+00 5.9038743192 Income -1.312611e-03 0.0014414600 Frost -1.966781e-02 0.0208304170 2.5 % 97.5 % (Intercept) -6.552191e+00 9.0213182149 Population 4.136397e-05 0.0004059867 Illiteracy 2.381799e+00 5.9038743192 Income -1.312611e-03 0.0014414600 Frost -1.966781e-02 0.0208304170 |
最適なモデルの選別
線型モデルの最適なモデルの選択を行うために、赤池情報量基準（AIC）を使って線型モデルの説明変数の組み合わせから、最適なモデルを見つける関数がMASSパッケージのstepAIC関数です。
stepAICの結果、PopulationとIlliteracyのモデルが最適なモデルであることが求まりました。
# AICをベースに最適なモデルを求める
r('library(MASS)')
r('fit<-lm(Murder ~ Population + Illiteracy + Income + Frost,data=states)')
r('stepAIC(fit, direction="backward")')
Call: lm(formula = Murder ~ Population + Illiteracy, data = states) Coefficients: (Intercept) Population Illiteracy 1.6515497 0.0002242 4.0807366 Call: lm(formula = Murder ~ Population + Illiteracy, data = states) Coefficients: (Intercept) Population Illiteracy 1.6515497 0.0002242 4.0807366 |
K-分割交差検証
オーバーフィッティングを防ぐためにK-分割交差検証を使用します。
K-分割交差検証は、サンプルデータをk個に分割し、K-1個を訓練データに、残る1個を検証用データとして回帰分析を繰り返し、K回の結果を平均して解を求めます。
#r('install.packages("bootstrap")')
r('library(bootstrap)')
# shrinkage関数をsourceコマンドで読み込む
filename = DATA+"shrinkage.txt"
r('source("%s")' % filename)
$value
function (fit, k = 10)
{
theta.fit <- function(x, y) {
lsfit(x, y)
}
theta.predict <- function(fit, x) {
cbind(1, x) %*% fit$coef
}
x <- fit$model[, 2:ncol(fit$model)]
y <- fit$model[, 1]
results <- crossval(x, y, theta.fit, theta.predict, ngroup = k)
r2 <- cor(y, fit$fitted.values)^2
r2cv <- cor(y, results$cv.fit)^2
ret <- paste("Original R-square =", r2, "\n")
ret <- paste(ret, k, "Fold Cross-Validated R-square =", r2cv,
"\n")
ret <- paste(ret, "Change =", r2 - r2cv, "\n")
return(ret)
}
$visible
[1] FALSE
$value
function (fit, k = 10)
{
theta.fit <- function(x, y) {
lsfit(x, y)
}
theta.predict <- function(fit, x) {
cbind(1, x) %*% fit$coef
}
x <- fit$model[, 2:ncol(fit$model)]
y <- fit$model[, 1]
results <- crossval(x, y, theta.fit, theta.predict, ngroup = k)
r2 <- cor(y, fit$fitted.values)^2
r2cv <- cor(y, results$cv.fit)^2
ret <- paste("Original R-square =", r2, "\n")
ret <- paste(ret, k, "Fold Cross-Validated R-square =", r2cv,
"\n")
ret <- paste(ret, "Change =", r2 - r2cv, "\n")
return(ret)
}
$visible
[1] FALSE
|
例では、shrinkage関数内でK-分割交差検証用の関数crossvalを使って、R-squareが0.06改善されたことを示しています。
# AICで求めたモデルに対し回帰分析を実施
r('fit <- lm(Murder ~ Population + Illiteracy, data=states)')
# shrinkageの実行
r('shrinkage(fit)')
[1] "Original R-square = 0.566832677066343 \n 10 Fold Cross-Validated R-square = 0.541458786180219 \n Change = 0.0253738908861243 \n" [1] "Original R-square = 0.566832677066343 \n 10 Fold Cross-Validated R-square = 0.541458786180219 \n Change = 0.0253738908861243 \n" |
|
|