Sageでグラフを再現してみよう:ギブス・サンプラー
この企画は、雑誌や教科書にでているグラフをSageで再現し、 グラフの意味を理解すると共にSageの使い方をマスターすることを目的としています。
今回は、計算統計Ⅱマルコフ連鎖モンテカルロ法とその周辺 のp169のギブス・サンプラーの例(図2)を題材にします。

図2について
図2は、n=100個の乱数をN(5, 1)から発生させて、事前分布$\mu \sim N(0, 1000), \sigma \sim IG(0.001/2, 0.001/2)$とおいてギブス・サンプリングを行った結果です。
条件付き事後分布
データが既存分布(今回の場合正規分布)を示している場合、ギブス・サンプリングを使って、 条件付き事後分布からサンプリングが可能になります。
平均$\mu$が分散$\sigma^2$の正規分布に従うとすると、事前分布$ \mu \sim N(\mu_0, \sigma^2_0), \sigma^2 \sim IG(n_0/2, S_0/2)$とすると、 $\mu$の条件付き事後分布は、以下のようになります。 $$ \mu | \sigma^2, x \sim N(\mu_1, \sigma^2_1), $$ $$ \sigma^{-2}_1 = \sigma^{-2}_0 + n \sigma^{-2}, \mu_1 = \frac{\sigma^{-2}_0 \mu_0 + n \sigma^{-2}\bar{x}} {\sigma^{-2}_0 + n \sigma^{-2}} $$
また、$\sigma^2$の条件付き事後分布は、以下のようになります。 $$ \sigma^2 | \mu, x \sim IG(n_1/2, S_1/2), $$ $$ n_1 = n_0 + n, S_1 = S_0 + \sum^{n}_{i = 1} ( x_i - \mu)^2 $$
ギブス・サンプリングのアルゴリズム
事後分布からのサンプリングアルゴリズムは、以下のようになります。
- 初期値($\mu^{(0)}, \sigma^{2(0)}$を決め、t = 1とする
- $\mu$の条件付き事後分布から、$\mu^{(t)}$をサンプリングする $$ \mu^{(t)} | \sigma^{2(t-1)}, x \sim N(\mu_1^{(t)}, \sigma^{2(t)}_1), $$ $$ \sigma^{-2(t)}_1 = \sigma^{-2}_0 + n \sigma^{-2(t-1)}, \mu_1^{(t)} = \frac{\sigma^{-2}_0 \mu_0 + n \sigma^{-2(t-1)}\bar{x}} {\sigma^{-2}_0 + n \sigma^{-2(t-1)}} $$
- $\sigma$の条件付き事後分布から、$\sigma^{2(t)}$をサンプリングする $$ \sigma^{2(t)} | \mu^{(t)}, x \sim IG(n_1/2, S_1^{(t)}/2), $$ $$ n_1 = n_0 + n, S_1^{(t)} = S_0 + \sum^{n}_{i = 1} ( x_i - \mu^{(t)})^2 $$
- t = t+1として、(2)に戻る
|
|
必要なライブラリの読み込み
今回の例では、逆ガンマ分布のサンプリングが必要ですので、psclパッケージのigamma関数を 使用することにしました。
[1] "pscl" "lattice" "MASS" "jsonlite" "ggplot2" "stats" "graphics" "grDevices" [9] "utils" "datasets" "methods" "base" [1] "pscl" "lattice" "MASS" "jsonlite" "ggplot2" "stats" "graphics" "grDevices" [9] "utils" "datasets" "methods" "base" |
テストデータの生成
例題の説明から、正規分布N(5, 1)からサンプルを100個生成します。 通常なら、
X = [gauss(5,1) for i in range(100)]とするところですが、常に同じサンプルが生成できるようにRealDistribution関数 (sage5.0から使えるようになった)を使ってテストデータを生成します。
生成したデータをプロットしています。
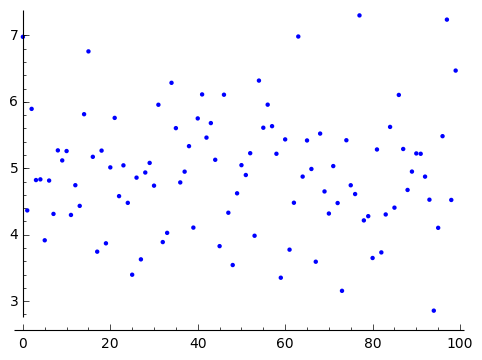
|
テストデータの分布
生成したデータをヒスとグラムで表示すると以下のようになっています。
|
|
IG関数の定義
$\sigma^2$の分布に逆ガンマ関数が使われているのは、その共役分布が正規分布であることに起因しています。
Sageには、逆ガンマ関数がないため、Rのrigamma関数を使って逆ガンマ分布のサンプリングをします。 IG関数は以下のようになります。
|
|
ギブス・サンプリングの初期設定
ギブス・サンプリングされた変数$\mu, \sigma^2$の値は、リストMu, Sigma2にセットします。
テストデータの個数n, xの平均をx_bar, $\mu_0$をmu_0、$\sigma^2_0$をsigma2_0に $n_0, S_0$をそれぞれ、n_0, S_0変数にセットします。
$sigma^2_0 = 1000$としているのは、事前分布情報がない場合、分散を大きく取って不確実性を 表現しています。
また、$n_0, S_0$を0.001と小さく取ることによって1回のサンプリングによる変動を小さくしています。
|
|
ギブス・サンプリングの実行
ギブス・サンプリングでは、最初の1000回までを稼働検査期間(buring in period) として、サンプリングから外しています。
その後の1000回をサンプリング期間とします。(モデルの複雑さなどで回数は異なります)
|
|
結果のプロット
$\mu, \sigma^2$の変動と密度分布を以下にプロットします。
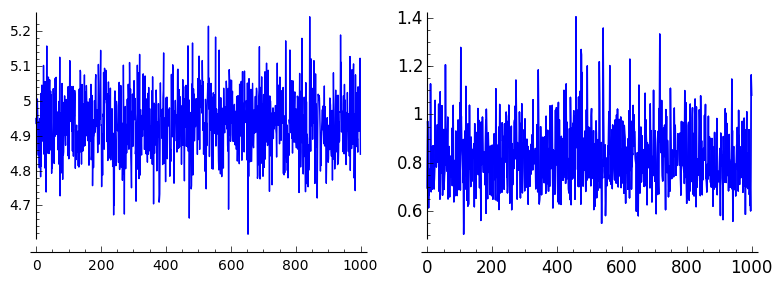
|
|
|
|
|
標本の散布図
標本の散布図を以下に示します。サンプリングによって$\mu, \sigma^2$が不変分布に収束していることが分かります。
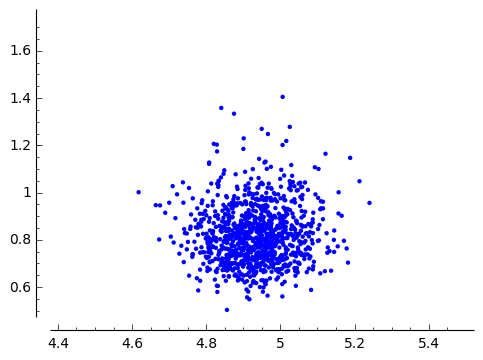
|
|
|


